104. Maximum Depth of Binary Tree

Question

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

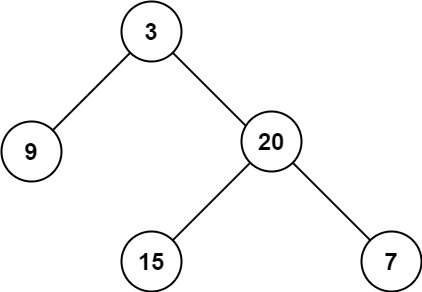
Input: root = [3,9,20,null,null,15,7]
Output: 3

Algorithm

Another simple question of binary search.

For such problem,

• think about what happens to a single node;
• Check the relation ship between node and the next node (or layer) to be traversed;
• Determine the stop condition, the base case.

For this question,

• Singe node start from node has a depth;
• Each time we hit the next level node, we add one (depth count);
• Base case is when we hit the leaf node where it's left and right is null;

We select the larger one from left and right side so there is a max function.

Or in reverse, for single node, the max depth start from it is 1(it's own layer) and the max depth of its children. And same logic to its children. So that's the place of recursion happens.

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}