110. Balanced Binary Tree

Published on July 19, 2023

Question

Given a binary tree, determine if it is height-balanced.

Example 1:

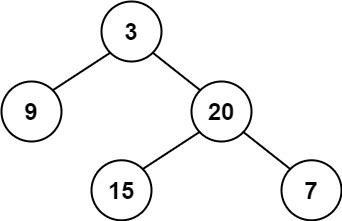
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

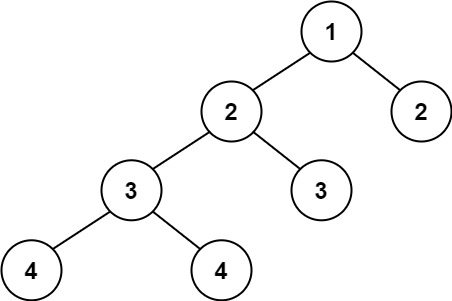
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Algorithm

This question you need to think about what is height balanced?

At first I thought it's the difference left max depth and right max length is no more than one.

But it's not right. The other condition is you need to make sure left and right subtrees are also height balanced.

You may need to ask interview what it is if you are not clear.

So translate the above sentence, we get the code below.

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        int left = height(root.left);
        int right = height(root.right);
        boolean leftTree = isBalanced(root.left);
        boolean rightTree = isBalanced(root.right);
        return leftTree && rightTree && Math.abs(left - right) <= 1;
    }
    
    private int height(TreeNode root) {
        if (root == null) return 0;
        if (root.left == null && root.right == null) return 1;
        return Math.max(height(root.left), height(root.right)) + 1;
    }
}