- Populating Next Right Pointers in Each Node
- Populating Next Right Pointers in Each Node II
Question1
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Example 1:
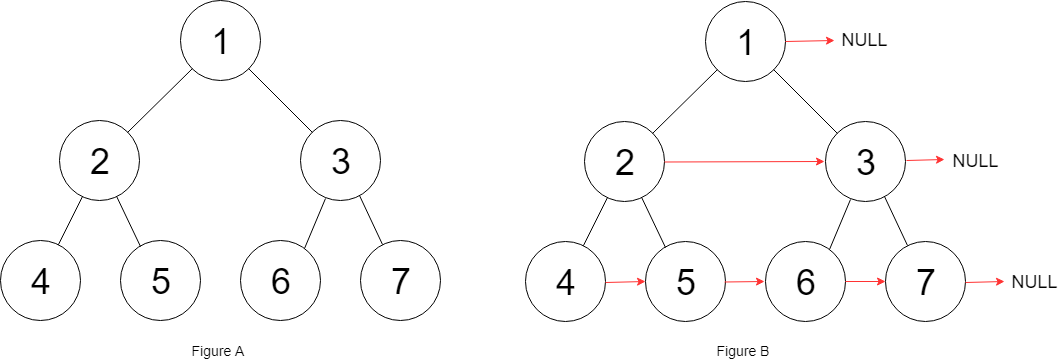
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
Example 2:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 212 - 1]. -1000 <= Node.val <= 1000
Follow-up:
- You may only use constant extra space.
- The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.
Algorithm1
For this problem there is an obvious way to solve it. You do a level order traversal and for each level of nodes, you connect them. Easy basket.
However, the follow up requires us to not use extra space, so a level order traversal is not applicable for it utilize a queue.
Actually we could think about the relationships of nodes, a node left will point to its right, and its right, firstly I though it would point to the its parent siblings left. However, this is not applicable to this scenario: (1, and 2 is ok but not 3)
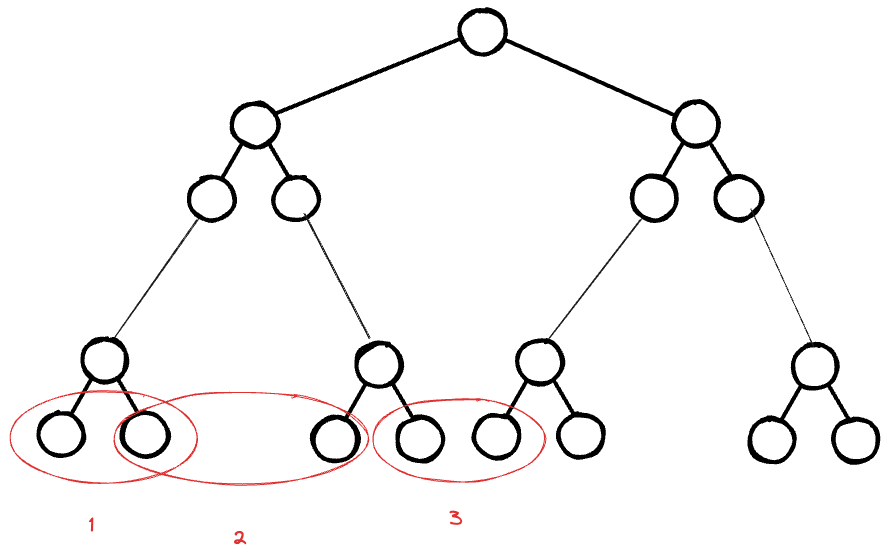
So I have to think about the other solutions.
Remember, we actually building these nodes relation levee by level so for level 5 we are ready have level 1-4 relation build. So in 3 scenario, the right node's parents next is the left child parent! What a relationship! We could utilize it in 2 as well. So all the relationship has figured out and we can start to code.
Code1
/* // Definition for a Node. class Node { public int val; public Node left; public Node right; public Node next; public Node() {} public Node(int _val) { val = _val; } public Node(int _val, Node _left, Node _right, Node _next) { val = _val; left = _left; right = _right; next = _next; } }; */ class Solution { public Node connect(Node root) { Queue<Node> queue = new LinkedList<>(); if (root == null) return root; queue.offer(root); while (!queue.isEmpty()) { int size = queue.size(); Node pre = null; for (int i = 0; i < size; i++) { Node cur = queue.poll(); if (pre != null) { pre.next = cur; } pre = cur; if (cur.left != null) queue.offer(cur.left); if (cur.right != null) queue.offer(cur.right); } } return root; } }
Follow up (Without Extra Space)
class Solution { public Node connect(Node root) { if (root == null) return root; if (root.left != null) root.left.next = root.right; if (root.right != null && root.next != null) root.right.next = root.next.left; connect(root.left); connect(root.right); return root; } }
Question2
Given a binary tree
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Algorithm2
This time we don't have a full binary tree where we can't regard the left and right is always exist. So I tried to compose a code that takes care of the null situations.
However, the issue is that, if there is not full, the next relationship will not build up when the current processing node is processed.
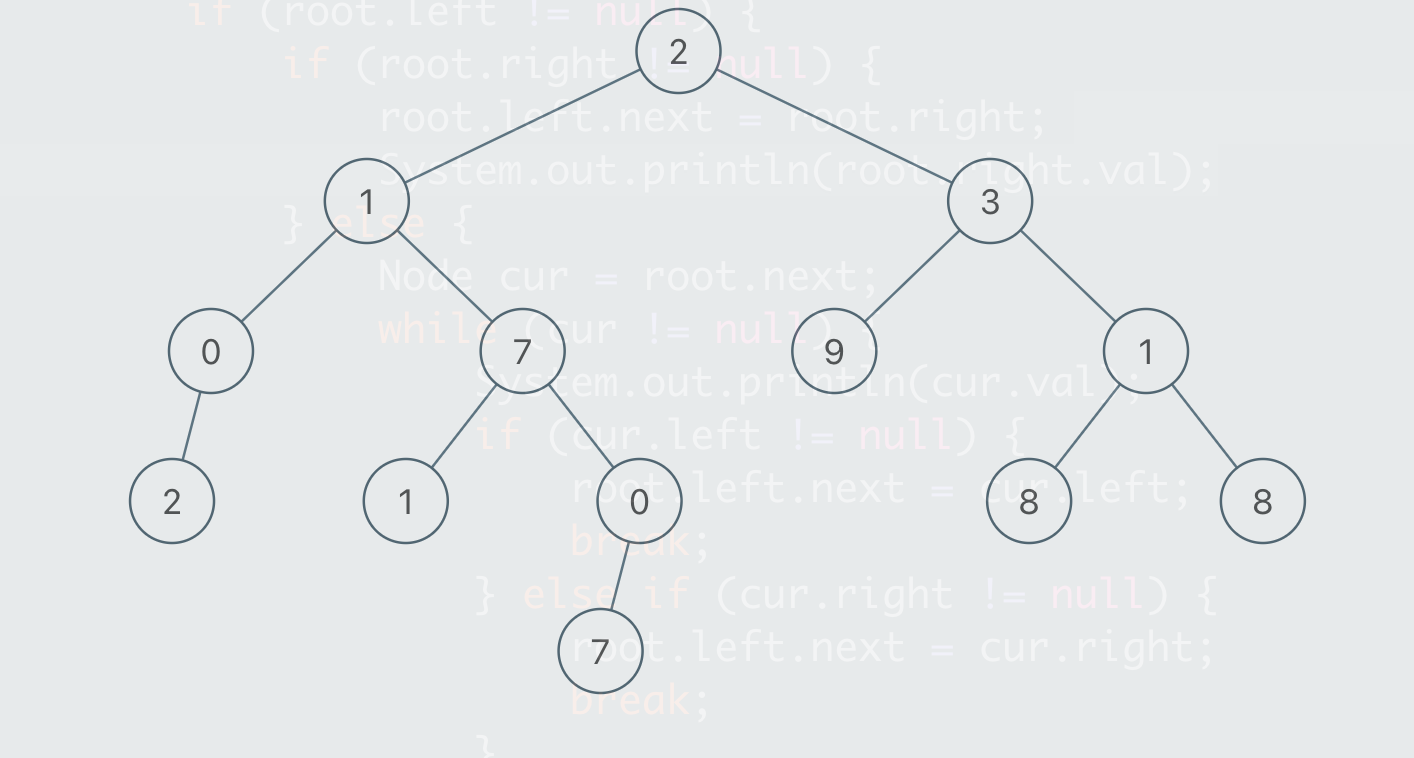
The node 7 and node9 hasn't build a next relationship when the children of node7 is processing thus node7's right child node0 cannot rely on node7's next and build relationship with node8(the left one).
Why this doesn't happen to the question1? In question1, it's a full binary tree, if we are processing above tree and node9 has left and right children, when processing node7, node7's right connect node9's left, and then process node3, node9 and when processing node9, it's left and right will be connected.
But in the question2, node9 has no child, when processing node7, its right child didn't have direct connection with the siblings children(node9's child), and thus cannot be find in the following loop by calling node0's next.
So other ways needs to be come up.
Actually to solve the issue in code2, we ca introduce a pre and always keep the prev node so we will not lose the pre even if they are far away(don't belong to the neighbor parent node). And handle the nodes level by level so we can keep the prev info and manipulate it.
Code2
class Solution { public Node connect(Node root) { if (root == null) return root; if (root.left != null) { if (root.right != null) { root.left.next = root.right; System.out.println(root.right.val); } else { Node cur = root.next; while (cur != null) { System.out.println(cur.val); if (cur.left != null) { root.left.next = cur.left; break; } else if (cur.right != null) { root.left.next = cur.right; break; } cur = cur.next; } } } if (root.right != null) { Node cur = root.next; while (cur != null) { System.out.println(cur.val); if (cur.left != null) { root.right.next = cur.left; break; } else if (cur.right != null) { root.right.next = cur.right; break; } cur = cur.next; } } connect(root.left); connect(root.right); return root; } }
Code3(👍🏻)
class Solution { public Node connect(Node root) { Node cur = root; Node pre = null; Node head = null; while (cur != null) { while (cur != null) { if (cur.left != null) { if (pre == null) { head = cur.left; } else { pre.next = cur.left; } pre = cur.left; } if (cur.right != null) { if (pre == null) { head = cur.right; } else { pre.next = cur.right; } pre = cur.right; } cur = cur.next; } cur = head; head = null; pre = null; } return root; } }