153. Find Minimum in Rotated Sorted Array && 154. Find Minimum in Rotated Sorted Array ||

1. Find Minimum in Rotated Sorted Array && 154. Find Minimum in Rotated Sorted Array ||

Question1

Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,2,4,5,6,7] might become:

• [4,5,6,7,0,1,2] if it was rotated 4 times.
• [0,1,2,4,5,6,7] if it was rotated 7 times.

Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], ..., a[n-2]].

Given the sorted rotated array nums of unique elements, return the minimum element of this array.

You must write an algorithm that runs in O(log n) time.

Algorithm1

O(logn) and sorted array, we know we are going to use binary search. So I check the possible sequence and potential result position, got:

• If the sequence is not rotated we do the same logic as binary search;
• If mid element is larger than right element, we go right side since we know there is a turning point;
• If left element is larger than mid element, we know there is a turning point so we go left side;

And then I found we left over one situation which is the mid element is smaller than both left and right, then it's the turning point and the smallest element.

Code1

class Solution {
    public int findMin(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (mid + 1 <= right && mid - 1 >= left) {
                if (nums[mid] <= nums[mid+1] && nums[mid] <= nums[mid-1]) {
                    return nums[mid];
                }
            }
            if (nums[mid] <= nums[right]) {
                right = mid - 1;
            } else if (nums[mid] > nums[right]) {
                left = mid + 1;
            } 
        }
        return nums[left];
    }
}

Question2

This question is a follow up question for leetcode 153. The input array contains duplicate elements.

Algorithm2

For this question, I have to admit that I didn't take too much efforts before I turned to the solutions provided by others.

Good news is the way it come up is same as mine. Bad news I didn't find how to deal with the duplicate elements. Well it's obvious, if we cannot decide, we just move one step until we can decide. Let's walk thought an example:

1. We may have mid(pivot in the graph) larger than right bound, then we know we need to to left side;

   

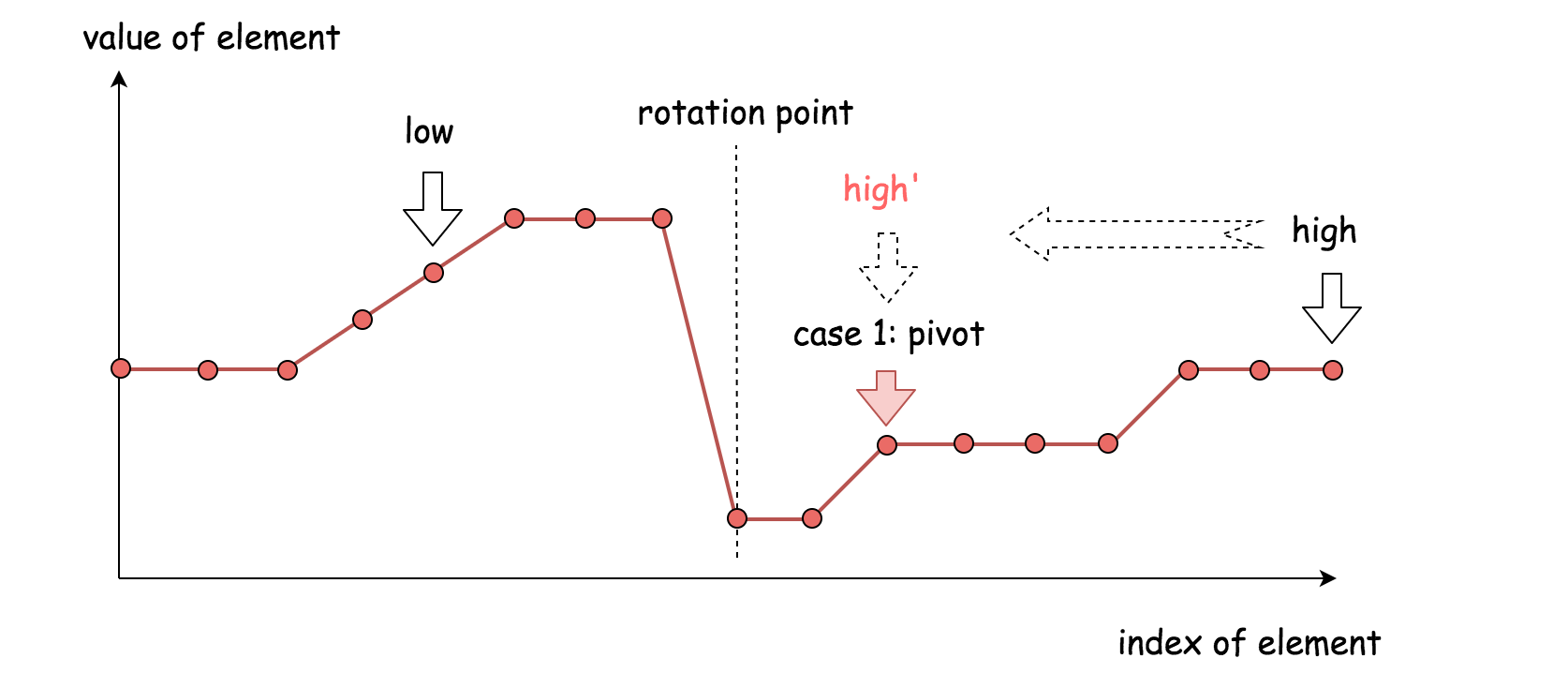
2. And if mid is smaller, we to the other side;

   

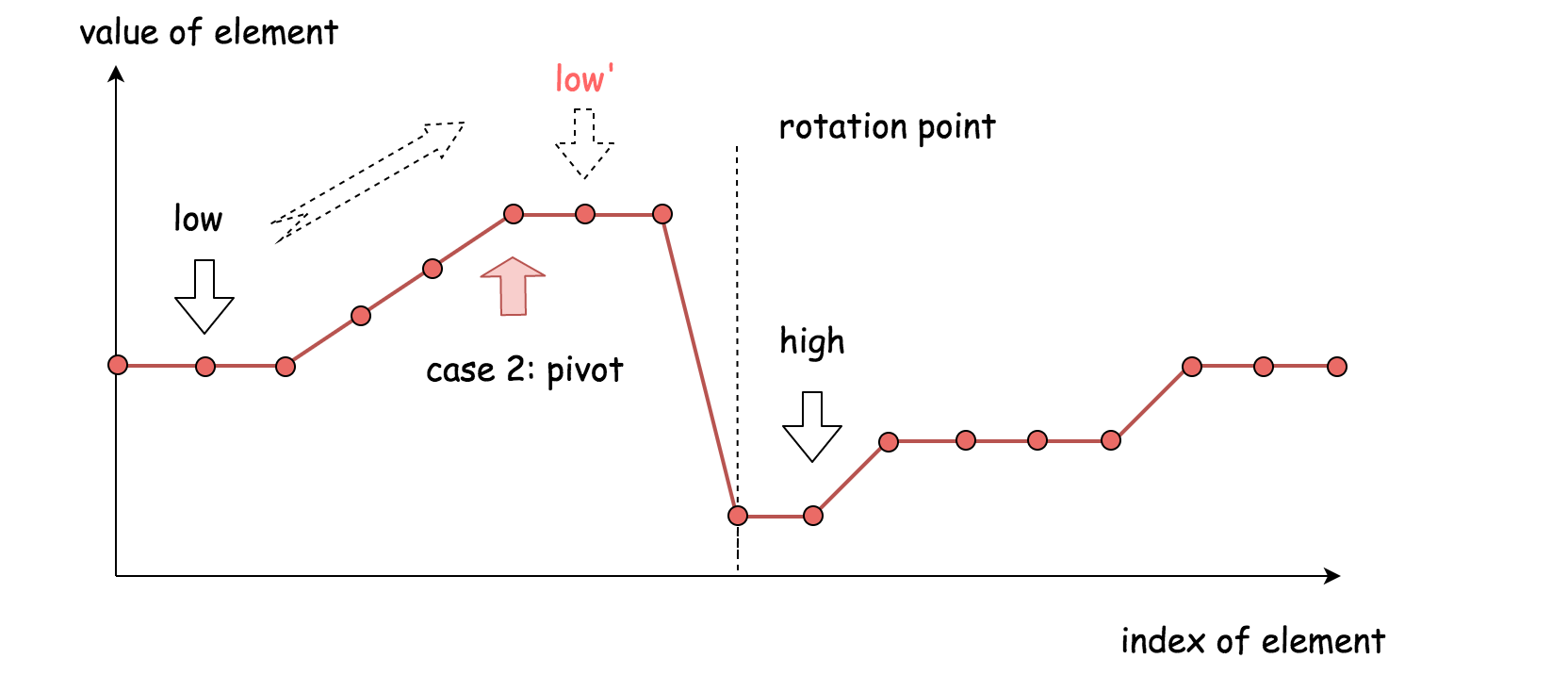
3. If they are equal, we move one step until we can decide the side;

   

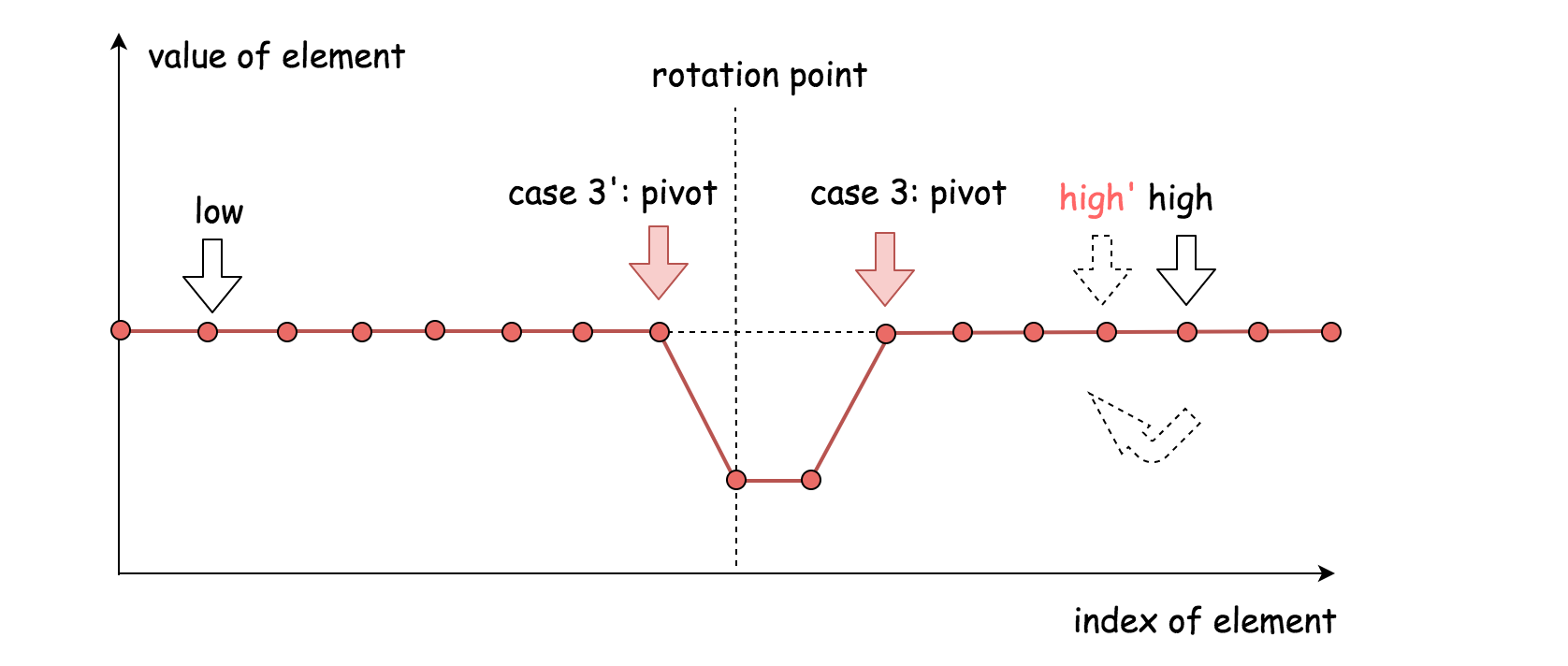
Code2

class Solution {
    public int findMin(int[] nums) {
        int left = 0, right = nums.length-1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[right]) {
                left = mid + 1;
            } else if (nums[mid] < nums[right]) {
                right = mid;
            } else {
                right--;
            }
        }
        return nums[left];
    }
}

Here is another wired combination, we use right boundary as nums.length - 1 and we use condition left < right, they are not a regular search combination, and the reason is (in my view):

Here is one way to think about this: we are aiming to find an element IN the array, so the final position of left or right must not out of bound. So we need to use nums.length - 1 as right.

Discuss also mentioned, sometimes we need to do slightly modification to accommodate the problem.