173. Binary Search Tree Iterator

Question

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

• BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
• boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
• int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:

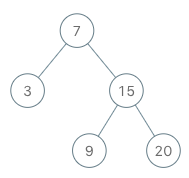
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // return 3
bSTIterator.next();    // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 20
bSTIterator.hasNext(); // return False

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 0 <= Node.val <= 106
• At most 105 calls will be made to hasNext, and next.

Algorithm

This question is an implementation question using in-order traversal. Rather than return at once, we are asked to return one each time we call the next.

So we don't calculate the result list by loop, instead we pause each time we got a result (node) from the stack, until next time next is called and we continue do the in-order traversal.

In traditional traversal, we loop by check of the stack is empty. This check is moved to the hasNext and the call next is guaranteed to be valid. But there is a scenario when the stack is empty, we still in the middle of traverse. So this condition is also regarded as the iterator has next value(because now the pointer cur is at the position of some right child, when calling next next, new nodes are pushed to the stack.

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class BSTIterator {
    Stack<TreeNode> stack;
    TreeNode cur;
    
    public BSTIterator(TreeNode root) {
        cur = root;
        stack = new Stack();
    }
    
    public int next() {
        while (cur != null) {
            stack.push(cur);
            cur = cur.left;
        }
        TreeNode node = stack.pop();
        if (node.right != null) {
            cur = node.right;
        }
        return node.val;
    }
    
    public boolean hasNext() {
        return !stack.isEmpty() || cur != null;
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * int param_1 = obj.next();
 * boolean param_2 = obj.hasNext();
 */