201. Bitwise AND of Numbers Range

Question

Given two integers left and right that represent the range [left, right], return the bitwise AND of all numbers in this range, inclusive.

Algorithm

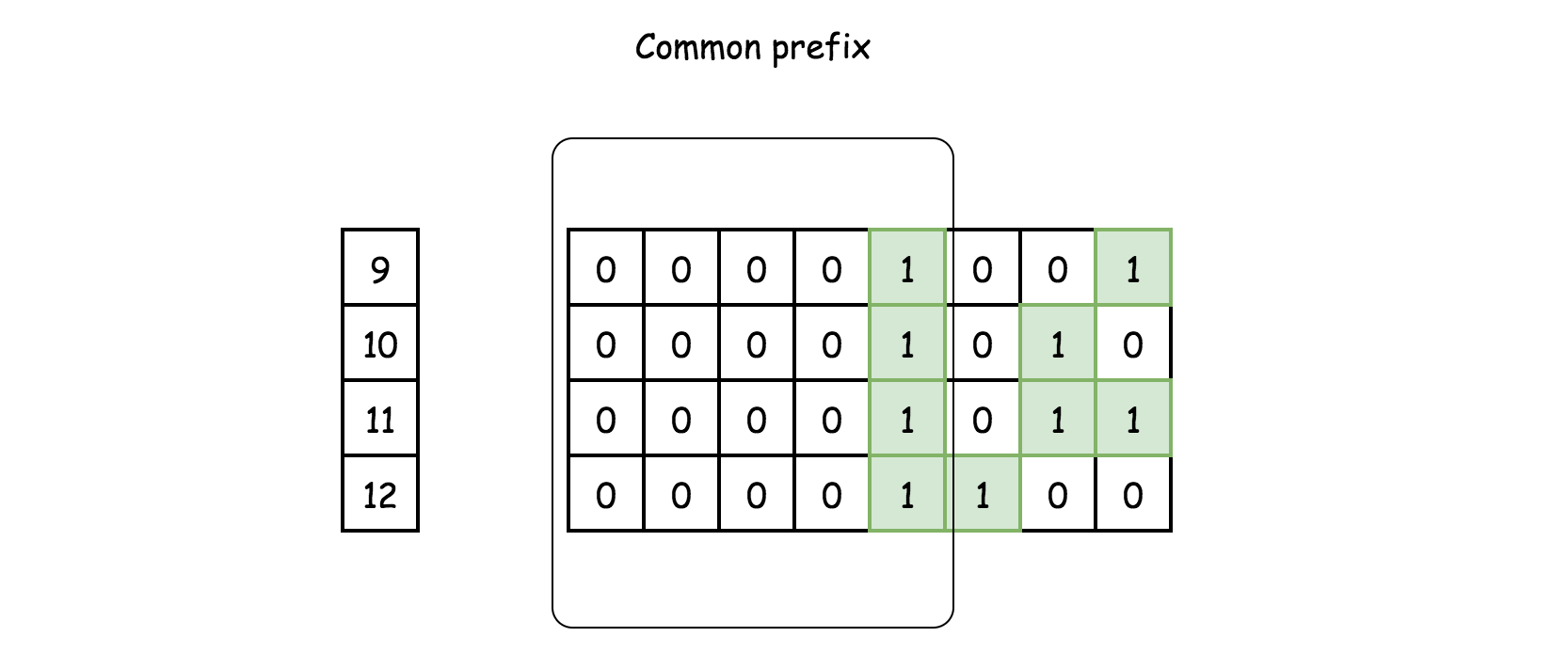
In the above example, one might notice that after the AND operation on all the numbers, the remaining part of bit strings is the common prefix of all these bit strings.

The final result asked by the problem consists of this common prefix of bit string as its left part, with the rest of bits as zeros.

More specifically, the common prefix of all these bit string is also the common prefix between the starting** and ending* numbers of the specified range (i.e.* 9 and 12 respectively in the above example).

As a result, we then can reformulate the problem as "given two integer numbers, we are asked to find the common prefix of their binary strings."

Code

This code will NOT pass the test and return TLE.

class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        int res = left;
        for (int i = left; i <= right; i++) {
            res &= i;
        }
        return res;
    }
}

~~So I guess we are asked to use an algorithm of time complexity O(1).~~

We will use an algorithm in time complexity less than O(n).

Code2

class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        int offset = 0;
        while (left != right) {
            left >>= 1;
            right >>= 1;
            offset++;
        }
        return left << offset;
    }
}