226. Invert Binary Tree

Published on July 13, 2023

Question

Given the root of a binary tree, invert the tree, and return its root.

Example 1:

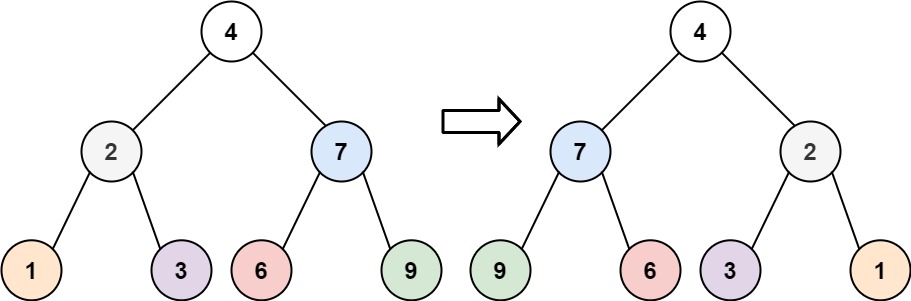
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Algorithm

This problem is obvious, for such problem(handle entire tree), we could keep eyes on single node action, and implement it with recursion.

For this question, What a node do is that it's left and right node change position, so as their children. So we do a swap for each node's left and right, and do such thing for the new left and right recursively until the node is null and has no child.

Code

This question is a little vague it didn't mention if we should create a new tree a do the invert in-place. So I have two implementation.

No in place:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;
        TreeNode newRoot = new TreeNode(root.val);
        helper(root, newRoot);
        return newRoot;
    }
    
    private void helper(TreeNode root, TreeNode newRoot) {
        if (root == null) return;
        if (root.right != null) newRoot.left = new TreeNode(root.right.val);
        if (root.left != null) newRoot.right = new TreeNode(root.left.val);
        helper(root.left, newRoot.right);
        helper(root.right, newRoot.left);
    }
}

In place:

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}