235. Lowest Common Ancestor of a Binary Search Tree

Question

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

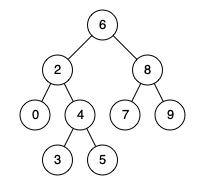
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Algorithm

This question is straightforward. We utilized the attribute of binary search tree, the left is smaller than the root and right is larger than the root.

So, if one node is larger than root and one node is smaller than root the LCA must be the root. Otherwise, if they are both smaller, then we look for the LCA in the left side and same as the right side.

If one of the node is equal to the root in recursion, then it's the LCA.

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root.val > p.val && root.val > q.val) {
            return lowestCommonAncestor(root.left, p, q);
        } 
        if (root.val < p.val && root.val < q.val) {
            return lowestCommonAncestor(root.right, p, q);
        } 
        return root;
    }
}