296. Best Meeting Point

Published on June 24, 2023

Wish you save and sound on Dragon Boat Day.

Question

Given an m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance**.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

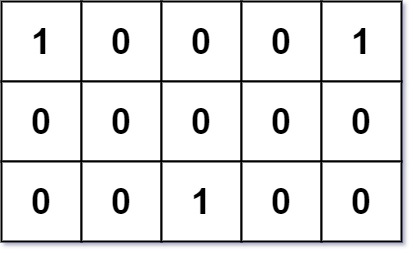
Input: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 6
Explanation: Given three friends living at (0,0), (0,4), and (2,2).
The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.
So return 6.

Example 2:

Input: grid = [[1,1]]
Output: 1

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 200
grid[i][j] is either 0 or 1.
There will be at least two friends in the grid.

Algorithm

Firstly I came up with the brute force way which is slow. So the Leetcode won't accept. The brute force way is keeping all the home location, and then traverse all the grids and find the one with shortest distance.
I will discuss this approach in detail. We have two things to figure out: the first one is why median? And the second is how do we implement.
1. According to the manhattan distance, the final distance is the sum of two dimensions, we could solve in one dimension and then sum the result.
2. First, we could know that, the meeting point must locate between left most point and right most point.
  1. Why? Say we have A, and C represent people, and B/D are the meeting points, meeting in B, the total distance is AB+BC, while meeting at D(outside AC), the distance is AC +CD, where CD is overlapped and can be avoid if they meet between them.
3. So we try mean of all the numbers in 1D.
  1. Case #3: 1-0-0-0-0-0-0-1-1
  2. Mean = 5 and total distance is 10, however, the shortest distance is 8 and best meeting point is 7.(according to a know example)
4. Another guess is median.
  1. Let's verify if it's the answer.Case #4: 1-1-0-0-1, the median is 1 and if we move the meeting point to 1 step right side, there are 2 nodes on the left side so the distance increase 2, and 1 node on the right side and the distance decrease 1, so the total distance increase 1.
  2. So we can conclude that: As long as there is equal number of points to the left and right of the meeting point, the total distance is minimized.
This method utilizing selection algorithm and select coordinates(median) in sorted order. I will not discuss this method too much here.
1. For even number 1's, it's same to meet in the either node of mid two 1's.
Finally it's the implementation.
1. We calculate the distance in 2 dimensions separately so we collect the x's and y's first;
2. Sort y's because we collect them row by row and they are not ordered with other rows;
3. Get the medians for x's and y's;
4. Calculate the distance for each dimension according to the median.

Code

Code1-TLE

Time complexity : O(m^2*n^2)

class Solution {
    public int minTotalDistance(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int res = Integer.MAX_VALUE;
        List<int[]> homes = new ArrayList<>();
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    homes.add(new int[]{i, j});
                }
            }
        }
        
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int dis = 0;
                for (int[] home : homes) {
                    dis += (Math.abs(home[0] - i) + Math.abs(home[1] - j));
                }
                res = Math.min(dis, res);
            }
        }
        return res;
    }
}

Code2

Time complexity: O(mn * logmn)

class Solution {
    public int minTotalDistance(int[][] grid) {
        List<Integer> rows = new ArrayList<>();
        List<Integer> cols = new ArrayList<>();
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] == 1) {
                    rows.add(i);
                    cols.add(j);
                }
            }
        }
        int row = rows.get(rows.size() / 2);
        Collections.sort(cols);
        int col = cols.get(cols.size() / 2);
        return minDist1D(rows, row) + minDist1D(cols, col);
    }
    
    private int minDist1D(List<Integer> points, int origin) {
        int dist = 0;
        for (int point : points) {
            dist += Math.abs(point - origin);
        }
        return dist;
    }
}

Code3

Time complexity: O(mn)

class Solution {
    public int minTotalDistance(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        List<Integer> I = new ArrayList<>();
        List<Integer> J = new ArrayList<>();
        
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(grid[i][j] == 1) {
                    I.add(i);
                }
            }
        }
        
        for(int j = 0; j < n; j++) {
            for (int i = 0; i < m; i++) {
                if(grid[i][j] == 1) {
                    J.add(j);
                }
            }
        }
        
        return min(I) + min(J);
    }
    
    private int min(List<Integer> list) {
        int i = 0; 
        int j = list.size() - 1;
        int sum = 0; 
        while(i < j) {
            sum += list.get(j--) - list.get(i++); 
        }
        return sum;
    }
}