31. Next Permutation

Question

Given a list a number, find its next permutation.

Algorithm

First method come to my mind is using backtracking to find all the permutation in order and find the one after the given array. Which require O(n!) time and O(n) space.

While we are required to find the next one in place.

So we watch the decision tree, try to find the pattern behind it.

To be honest, I didn't come up with it completely before I turned to the standard answer. (The thing I missed is I swap a[i] and a[i-1])

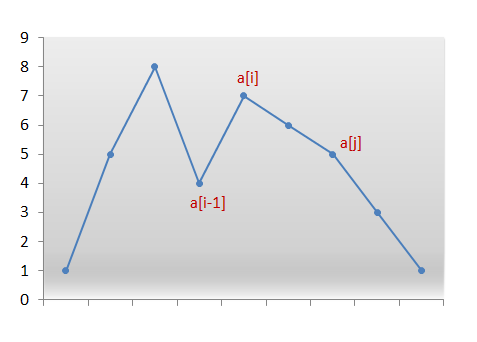
The next permutation is you go through the array and find the first pair of number where a[i] > a[i -1], and then you go through all the elements and find the one that just larger that a[i], swap them, and reverse all the elements after a[i] . The purpose of reverse the right side element of a[i] is we need to get smallest one after swap so that's would be smallest one.

while scanning the numbers from the right, we simply kept decrementing the index until we found the pair a[i] a[i-1] where a[i] > a[i-1] Thus, all numbers to the right of a[i-1 were already sorted in descending order. Thus we only need reverse.

Code

class Solution {
    public void nextPermutation(int[] nums) {
        if (nums == null || nums.length == 0 || nums.length == 1) {
            return;
        }
        // find the pair 
        int i = nums.length - 2;
        while (i >= 0 && nums[i + 1] <= nums[i]) {
            i--;
        }
            
        if (i >= 0) {
            // looks for the one just larger than the smaller number nums[i-1]
            int j = nums.length - 1;
            while (nums[j] <= nums[i]) {
                j--;
            }
            swap(nums, i, j);
        } 
        // reverse
        i = i + 1;
        int j = nums.length - 1;
        while (i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
        
    }
    
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}