311. Sparse Matrix Multiplication

Published on June 5, 2023

Question

Given two sparse matrices mat1 of size m x k and mat2 of size k x n, return the result of mat1 x mat2. You may assume that multiplication is always possible.

Example 1:

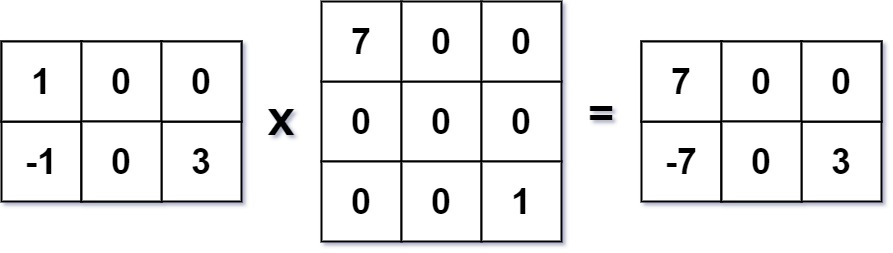
Input: mat1 = [[1,0,0],[-1,0,3]], mat2 = [[7,0,0],[0,0,0],[0,0,1]]
Output: [[7,0,0],[-7,0,3]]

Example 2:

Input: mat1 = [[0]], mat2 = [[0]]
Output: [[0]]

Constraints:

m == mat1.length
k == mat1[i].length == mat2.length
n == mat2[i].length
1 <= m, n, k <= 100
-100 <= mat1[i][j], mat2[i][j] <= 100

Algorithm

First you need to know what's matrix, then you need to know how to do the matrix multiplication.

This graph is the key:

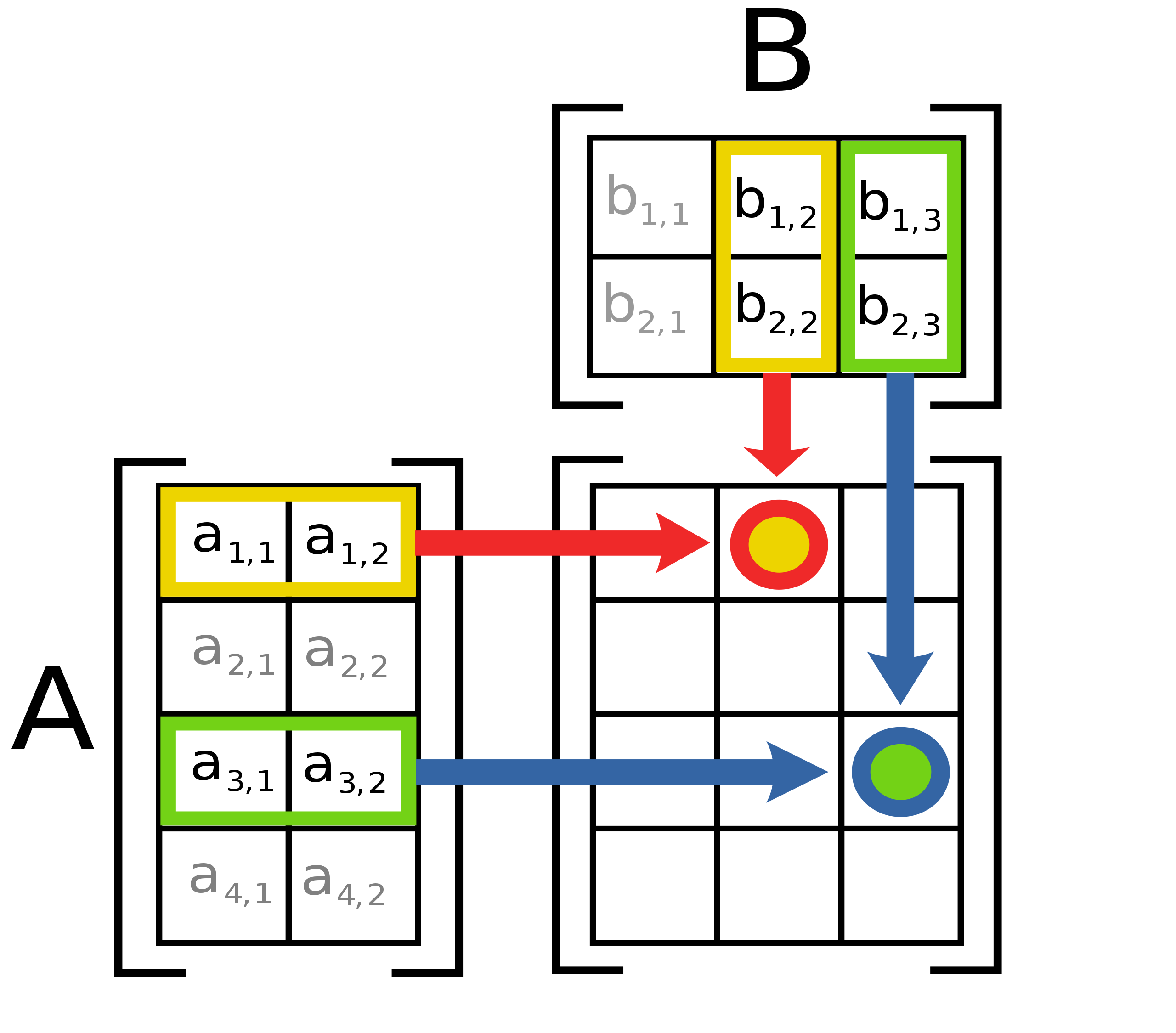
Matrix multiplication diagram 2.svg

The logic behind the scene is worth to discuss. What do this and what's the meaning.

The steps of implementation can be found in the wiki page or the graph.

Code

class Solution {
    public int[][] multiply(int[][] mat1, int[][] mat2) {
        int m = mat1.length;
        int k = mat1[0].length;
        int n = mat2[0].length;
        int[][] res = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < k; j++) {
                int num = mat1[i][j];
                for (int x = 0; x < n; x++) {
                    res[i][x] += num * mat2[j][x];
                }
            }
        }
        return res;
    }
}

However, the matrix we use to calculate is a sparse matrix which we could utilize this attribute and reduce the calculation a little bit.

class Solution {
    public int[][] multiply(int[][] mat1, int[][] mat2) {
        int m = mat1.length;
        int k = mat1[0].length;
        int n = mat2[0].length;
        int[][] res = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < k; j++) {
                if (mat1[i][j] != 0) {
                    int num = mat1[i][j];
                    for (int x = 0; x < n; x++) {
                        if (mat2[j][x] != 0) {
                            res[i][x] += num * mat2[j][x];
                        }
                    }
                }
            }
        }
        return res;
    }
}