329. Longest Increasing Path in a Matrix

Question

Given an m x n integers matrix, return the length of the longest increasing path in matrix.

From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

Example 1:

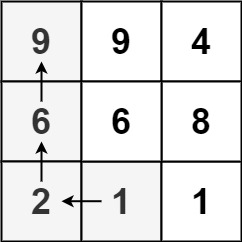
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

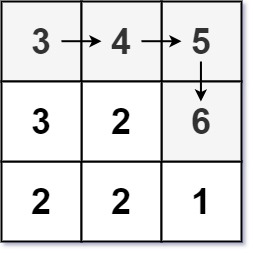
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Example 3:

Input: matrix = [[1]]
Output: 1

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 231 - 1

Algorithm

1. Naive flood filled algorithm will case a time limit exceed. Code1

2. If you think about the first solution, you may find when you traveling the matrix, some grid may be traversed repeatedly. So you may want utilize memorization to prune the unnecessary operations.

   In the code2, I made a huge optimized both in code and algorithm. In Algorithm, the code 1 worst case is O(2^m * 2^n), and space is O(mn), while the code2 is O(mn) for both time and space. Because in the second algorithm, each grid will be touched once and only once due to the memo. In the code1, each grid will be travelled to the end if it's worst case.

   In code, I use the direction array to avoid repetition in the code1. And the made the DFS itself return the desired value instead of introduce a new value carried with the function.

   The implementation would be we go through each node, and then check if their neighbors has a recalculated result, if yes, we simply get that one and add one step(or level); if not, we do a DFS to its neighbor. In the DFS, we keep updating the memo to get the result for each grid. If you are going next level, we add the result one step.

3. There is another solution which utilize the dynamic programming. But before you dive into DP, since the grid has dependencies on its neighbors, so the elements you manipulate in DB should be sorted first.

   Such dependency sorting is topological sort.

   Personally I think this is not that hard to implement but the more algorithm you involve in a solution, the higher chance you will get an error. So if you goal is to solve it, just use the algorithm2. That's enough.

Code1(Naive DFS)(TLE)

class Solution {
    int res;
    public int longestIncreasingPath(int[][] matrix) {
        res = 1;
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                dfs(matrix, i, j, 1);
            }
        }
        return res;
    }
    
    private void dfs(int[][] matrix, int i, int j, int level) {
        if (i - 1 >= 0) {
            if (matrix[i-1][j] > matrix[i][j]) {
                dfs(matrix, i - 1, j, level + 1);
            }
        }
        if (i + 1 < matrix.length) {
            if (matrix[i+1][j] > matrix[i][j]) {
                dfs(matrix, i + 1, j, level + 1);
            }
        }
        if (j - 1 >= 0) {
            if (matrix[i][j-1] > matrix[i][j]) {
                dfs(matrix, i, j - 1, level + 1);
            }
        }
        if (j + 1 < matrix[0].length) {
            if (matrix[i][j+1] > matrix[i][j]) {
                dfs(matrix, i, j + 1, level + 1);
            }
        }
        
        res = Math.max(res, level);
    }
}

Code2

class Solution {
    int[][] memo;
    int m, n;
    private static final int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    public int longestIncreasingPath(int[][] matrix) {
        int res = 1;
        m = matrix.length;
        n = matrix[0].length;
        memo = new int[m][n];
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                res = Math.max(res, dfs(matrix, memo, i, j));
            }
        }
        return res;
    }
    
    private int dfs(int[][] matrix, int[][] memo, int i, int j) {
        if (memo[i][j] != 0) {
            return memo[i][j];
        }
        for (int[] dir : dirs) {
            int x = i + dir[0], y = j + dir[1];
            if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {
                memo[i][j] = Math.max(memo[i][j], dfs(matrix, memo, x, y));
            }
        }
        return ++memo[i][j];
        
    }
}