337. House Robber III

Question

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.

Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police**.

Example 1:

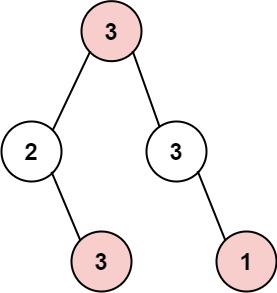
Input: root = [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Algorithm

I spend 20min thinking the algorithm, but failed. First I was impacted by the other question of house robber, think dynamic programming is a good way to solve the problem, however, for such kind of binary tree question, it seems the main stream of it is still the tree manipulation.

Restart from the tree perspective, it becomes more clear. However, it failed first time due to TLE. Too much recursion and repeat calculation, so tree + recursion problem, or even recursion, we should try to think about the memorization optimization.

For this question, you have two options for each node but it not that easy, the option also depends on the parent adjacent node's choice. If the parent is robbed, the children must not be rob; if the parent is not robbed, the children have two options.

So translated to Java code, it's like below: for each node we calculated the result both for if it's robbed, and not robbed and get the larger one. And for its child we utilize recursion and hide the details on how the children and grandsons calculation.

Code

This code is TLE...

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        return Math.max(helper(root, true), helper(root, false));
    }
    
    private int helper(TreeNode root, boolean isRobbed) {
        if (root == null) return 0;
        int notRobLeft = helper(root.left, false);
        int notRobRight = helper(root.right, false);
        int robLeft = helper(root.left, true);
        int robRight = helper(root.right, true);
        if (isRobbed) {
            return root.val + notRobLeft + notRobRight;
        } else {
            int leftMax = Math.max(robLeft, notRobLeft);
            int rightMax = Math.max(robRight, notRobRight);
            return leftMax + rightMax;
        }
    }
}

The problem is here in such recursion solution, we traverse a subtree multiple times thus causing redundant calculation. We may use memorization to prune.

class Solution {
    Map<TreeNode, Integer> memo = new HashMap<>();
    public int rob(TreeNode root) {
        if (root == null) return 0;
        if (memo.containsKey(root)) return memo.get(root);
        int doRob = root.val + (root.right == null ? 0: rob(root.right.left) + rob(root.right.right)) + (root.left == null ? 0: rob(root.left.left) + rob(root.left.right));
        int noRob = rob(root.left) + rob(root.right);
        int res = Math.max(doRob, noRob);
        memo.put(root, res);
        return res;
    }
}