378. Kth Smallest Element in a Sorted Matrix

Published on June 14, 2023

Question

Given an n x n matrix where each of the rows and columns is sorted in ascending order, return the kth smallest element in the matrix.

Note that it is the kth smallest element in the sorted order, not the kth distinct element.

You must find a solution with a memory complexity better than O(n2).

Example 1:

Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: The elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8th smallest number is 13

Algorithm

See the below each explanation.

Code

Code1

I use a priority queue to store all the numbers and pop them according to the index.

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        // 1. pq nlogn time, n space, not utilizing the sorted order in x and y;
        PriorityQueue<Integer> pq = new PriorityQueue();
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                pq.offer(matrix[i][j]);
            }
        }
        
        while (k-- > 1) {
            pq.poll();
        }
        return pq.poll();
        
    }
}

Code2

In my submission history and the answer provided by the leetcode, when they are using the priority queue, they also put the index info into the queue. I'm not fully understand this.

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        //solution 1 qriorityqueue 
        // space : O(n) time O(nlogn)
        PriorityQueue<Tuple> pq = new PriorityQueue<>(matrix.length, (a, b) -> (a.val - b.val));
        for(int i = 0; i < matrix.length; i++) {
            pq.offer(new Tuple(0, i, matrix[0][i]));
        }
        for(int i = 0; i < k - 1; i++) {
            Tuple tuple = pq.poll();
            if(tuple.x == matrix.length - 1) continue;
            pq.offer(new Tuple(tuple.x + 1, tuple.y, matrix[tuple.x + 1][tuple.y]));
        }
        return pq.poll().val;
    }
    public class Tuple{
        int x, y, val;
        public Tuple(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
    }
}

Code3

I also notice that each row is sorted, though I have no idea how to use binary search to tackle the problem. Thanks to the blog, who gives a clear walk through of the binary search process.

If you go through this algorithm roughly, you will have a question: Overall the number is not sorted, how do they determine the mid number?

Actually this algorithm doesn't really use the real number, it use the number count. Let walk through it.

We know the matrix[0][0] is the smallest number since in its right side and downside, all the numbers are larger, and thus matrix[n-1][n-1] is the largest in the matrix. So we are going to find the k-th largest number between them.
Each loop we will get the mid number and find its rank in the matrix. If this rank is smaller than k, we know that the number is smaller than the k-th number, we shrink the range to [start, mid]; if the mid number rank is larger than k, which means the mid number is larger than the k-th number and we need to go to [mid+1, end] to find the number.
1. We use mid number, but the number may not be in the matrix. What we are looking for is the number count that is smaller/larger than that mid, and shrink the search range until we only have 1 number in the range.
2. Let's go through an example, find the 21th smallest number.
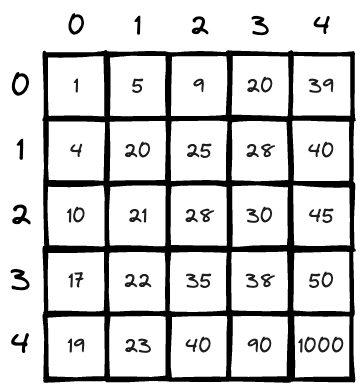
  1. We search range[1, 1000], mid number is 500, and we got 24 numbers smaller than 500, and the 21th we are looking for is smaller than 24, so we should shrink the search range in the first half, [1, 500];
  2. Then we look for range [1, 500], calculate mid number 250, and there are 24 number smaller than 250, which means 250 is the 24th smallest number; thus the range shrink to the [1, 125];
  3. Then we look for range [1, 125], calculate mid number 63, and there are 23 number smaller than 125, which means 125 is the 23rd smallest number; thus the range shrink to the [1, 63];
  4. Then we look for range [1, 63], calculate mid number 33, and there are 16 number smaller than 63, which means 63 is the 16th smallest number, which means our search range should become [33, 63];
  5. Then we look for range [33, 63], calculate mid number 48, and there are 22 number smaller than 48, which means 48 is the 22nd smallest number, which means our search range should become [33, 48];
  6. Then we look for range [33, 48], calculate mid number 40, and there are 21 number smaller than 40, which means 40 is the 21st smallest number, target rank! But we cannot confirm that 40 is in the matrix. So we continue narrow down the range to [33, 40];
  7. Then we check range [33, 40], mid number is 36 and it's rank is 18 so we know too much;
  8. Then we check range [37, 40], mid number is 38 and it's rank is 18 so we know too much;
  9. Then we check range [39, 40], mid number is 38 and it's rank is 19 so we know too much;
  10. Then we get range [40, 40], return it.
Now it becomes how do we count the number that are smaller than the mid number?
1. Maybe leetcode 240 is a good start for this question to search target number in a 2D-matrix.
2. We start from left down corner and count how many numbers are smaller.
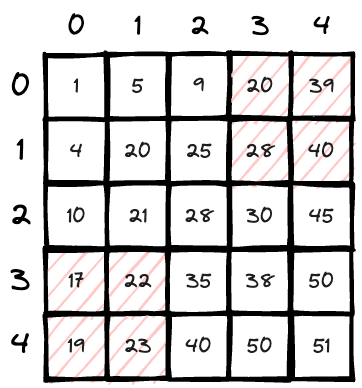
3. Lets walk through an example: find how many numbers are smaller than 20
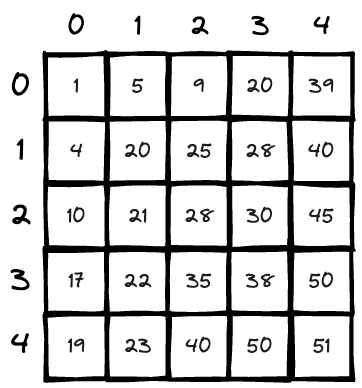
  1. We use count to store the number;
  2. We are starting from matrix[4][0] which is 19 and is smaller than 20, we know the numbers above it are larger, so the count += 5, which is 5 now. And to get closer to 20, we move the position rightward;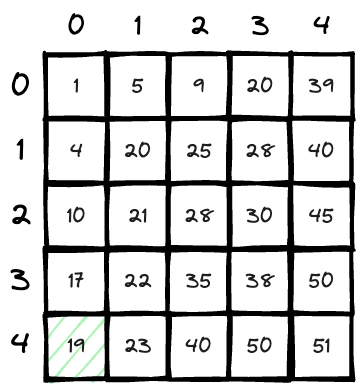
  3. Now we have matrix[4][1] > 20, so we go upwards for a smaller one; count = 5;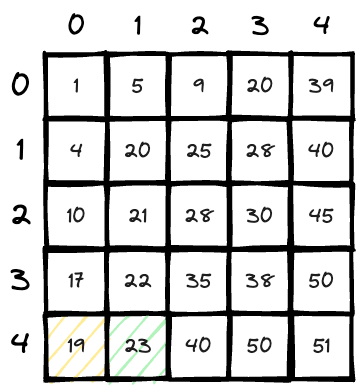
  4. Now we have matrix[3][1] > 20, so we go upwards for a smaller one; count = 5;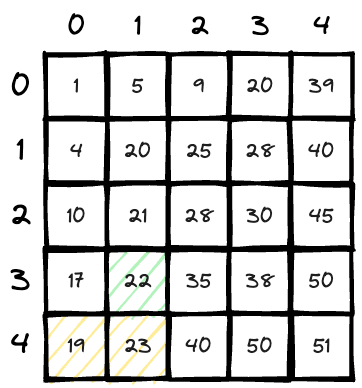
  5. Now we have matrix[2][1] > 20, so we go upwards for a smaller one;count = 5;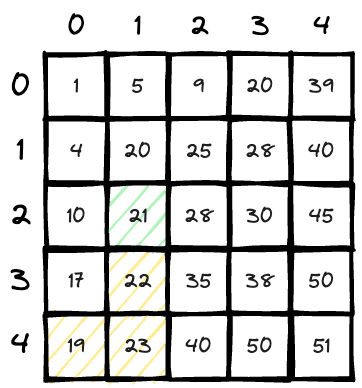
  6. Now we have matrix[1][1] <= 20, the number above it and in the left side are smaller than it, we came from right(larger side), so we go to right side to find a larger one(the final destination is the right above area); count += 2; count = 7;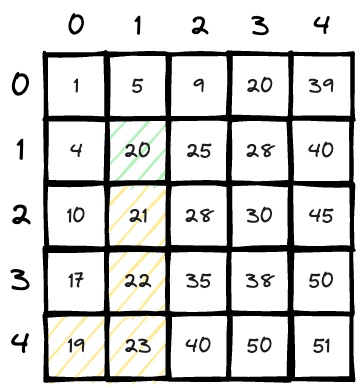
  7. Now we have matrix[1][2] > 20, so we go upwards for a smaller one; count = 7;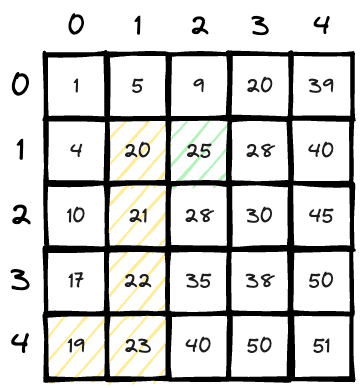
  8. Now we have matrix[0][2] <= 20, the number above it and in the left side are smaller than it, we came from right(larger side), so we go to right side to check if there is a larger one(the final destination is the right above area); count += 1; count = 8;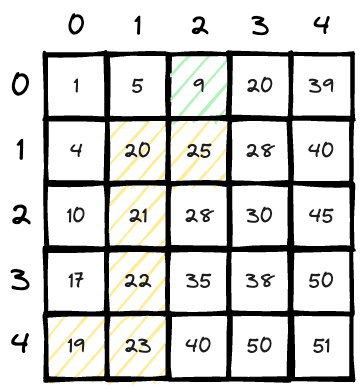
  9. Now we are at matrix[0][3]<=20. So we need to check if there are larger number in the right above area; so we go right; count += 1; count = 9;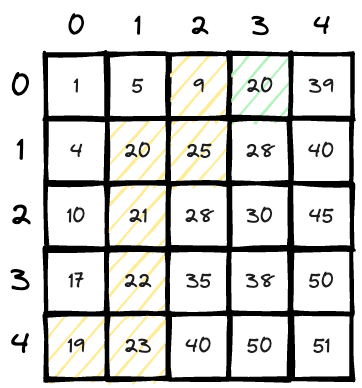
  10. Now we are at matrix[0][4] > 20. And we how nowhere to go (we are from left, and downside is even larger ones). count = 9.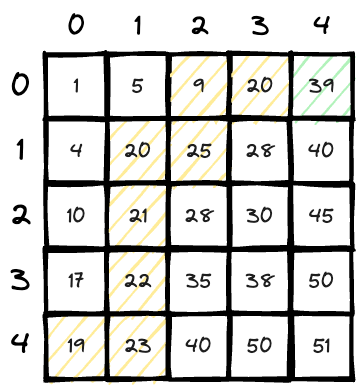
  11. Thus, all the smaller number are found, count = 9; red marked all the grids we counted.
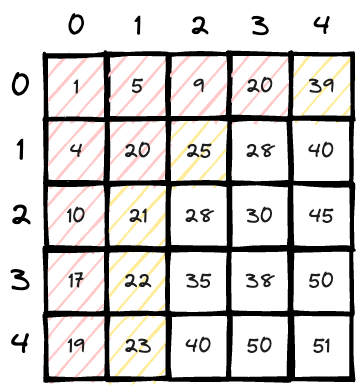
  12. The reason of each direction choose is that, for number 28, it's right upper area and left downside area are not guaranteed to be larger or smaller than it. So our count helper would go thought these areas to ensure we get all the qualified numbers.

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int start = matrix[0][0];
        int end = matrix[matrix.length-1][matrix[0].length-1]+1;
        while(start<end) {
            int mid = start+(end-start)/2;
            int count = 0;
            int j = matrix[0].length-1;
            for(int i = 0;i<matrix.length;i++) {
                while(j>=0 && matrix[i][j] > mid) j--;
                count += (j+1);
            }
            
            if(count >= k) {
                end = mid;
            } else {
                start = mid+1;
            }
        }
        return start;
    }
}

Time complexity is O(n*log(max-min)).

Code4(My code)

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int n = matrix.length;
        int left = matrix[0][0];
        int right = matrix[n-1][n-1];
        while (left < right) {
            int mid = left + (right - left) / 2;
            int count = helper(matrix, mid);
            if (count >= k) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
    private int helper(int[][] matrix, int num) {
        int n = matrix.length;
        int count = 0;
        int i = n - 1;
        int j = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] <= num) {
                count += (i+1);
                j++;
            } else {
                i--;
            }
        }
        return count;
    }
}