452. Minimum Number of Arrows to Burst Balloons

Problem

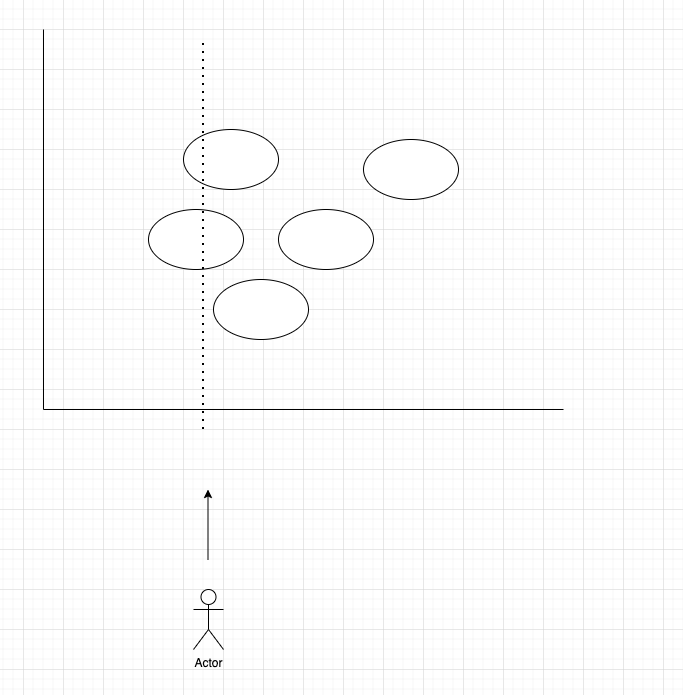
This problem looks complicated to describe, so look at it more closely. We have a bunch of balloons, 🎈 staggered in front of you, you shoot one arrow at a time, when the balloons are not overlapping, one arrow can only shoot through one balloon; when the balloons are overlapping, one arrow can shoot through them all. Ask how many arrows are needed to shoot through all the balloons. A diagram of this topic is clear at a glance.

Algorithms

Seeing the most value can be considered using greedy thinking.

Dynamic programming is actually also an idea to consider when you see the most value. Of course there are some differences between the two, and the final decision is whether to use greedy thinking or dynamic programming.

Also, we are talking about "ideas" here, not algorithms. Because this is an idea, a direction, not a specific algorithm.

This topic has the most value, use greedy thinking to try to consider. First find the local optimal solution, then iterate forward until the end.

As we can see from the figure above, we can iterate through the balloons from left to right (sorting first), and then when a balloon does not overlap with the previous balloon we can move to the new balloon and ignore the previous balloon (the previous result has been saved).

Here we first need to sort the balloons (according to their end position or right border), at this time will need to consume an arrow; then continue to look behind the balloon, if the balloon behind the overlap with the previous one, that is, the left border of the back is smaller than the current right border, then they can be shot by the same arrow, the cycle continues; when encountered no overlap balloon. That is, the left boundary of the balloon is greater than the current right boundary, at this time an arrow has not been able to pierce them, the new balloon needs another arrow, the result increases one, and at this time the new right boundary is the new right boundary of this balloon, we have to continue to look at the left boundary of the balloon behind him prevail.

Code

class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points == null || points.length == 0 || points[0] == null || points[0].length == 0) {
            return Integer.MAX_VALUE;
        }
        
        int res = 1;
        Arrays.sort(points, (a, b) -> {
            if (a[1] == b[1]) return 0;
            if (a[1] < b[1]) return -1;
            return 1;
        });
        int end = points[0][1];
        
        for (int i = 1; i < points.length; i++) {
            if (points[i][0] > end) {
                res++;
                end = points[i][1];
            } 
        }
        return res;
    }
}

The code before this topic, can't pass the test anymore, because before for array sorting use Arrays.sort(points, (a, b) -> (a[1] - b[1])); for larger numbers, such as [[-2147483646, -2147483645], [2147483646, 2147483647]], the result of their operations in anonymous functions may cause overflow, which in turn may affect the correctness of the result.

问题

这个问题看起来描述的复杂，要多仔细看一下。就是我们有一堆气球，🎈交错的排列在你的面前，你每次射一支箭，当气球没有重叠，一支箭只能射穿一个气球；当气球重叠，一支箭可以把他们都射穿。问最少需要多少支箭射穿全部气球。这个题目画个图一目了然：

算法

看到求最值可以考虑使用贪心思想。

动态规划其实也是看到最值的时候可以考虑的一种思路。当然这两者存在一些区别，最终以决定使用贪心思想还是动态规划思想。

另外这里说的是“思想”而非算法。因为这是一种思路，指导方向，而非一个具体的算法。

这个题目有求最值，使用贪心思路去尝试考虑一下。先求局部最优解，然后向前迭代，直到最后。

我们根据上图可以看到，我们可以从左到右去遍历这些气球（先排序），然后当一个气球与前一个气球不重叠的时候我们可以移动到新的的气球，而不用管之前的气球了（之前的结果已经保存）。

这里我们首先需要将气球们排序（按照他们的结束位置或者是右边界），此时将需要消耗一支箭；然后继续看后面的气球，如果后面的气球与前面的重叠，也即后面的左边界小于当前的右边界，那么他们可以被同一支箭射穿，循环继续；当遇到没重叠的气球。即气球的左边界大于当前的右边界，此时一支箭已经不能戳穿他们了，新的气球需要另一支箭，结果增加一个，并且此时新的右边界是新的这个气球的右边界，我们要依他为准继续看后面的气球的左边界了。

代码

class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points == null || points.length == 0 || points[0] == null || points[0].length == 0) {
            return Integer.MAX_VALUE;
        }
        
        int res = 1;
        Arrays.sort(points, (a, b) -> {
            if (a[1] == b[1]) return 0;
            if (a[1] < b[1]) return -1;
            return 1;
        });
        int end = points[0][1];
        
        for (int i = 1; i < points.length; i++) {
            if (points[i][0] > end) {
                res++;
                end = points[i][1];
            } 
        }
        return res;
    }
}

这个题目之前的代码，无法通过测试了，因为之前对于数组排序使用的是 Arrays.sort(points, (a, b) -> (a[1] - b[1])); 对于较大的数字，例如[[-2147483646, -2147483645], [2147483646, 2147483647]], 他们在匿名函数中的运算结果，可能会造成overflow，进而会影响结果的正确性。