84. Largest Rectangle in Histogram

Published on May 25, 2023

Question

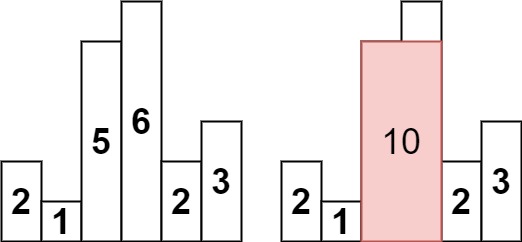
给定一个柱状图每个柱子的高度，每个柱子宽度为1，求这个图中最大矩形的面积。

Algorithm1

这个题目挺值得盘一盘的。我一开始没做出来，看记录也只提交过一次，但是他是栈类型题目中最难的一种，也比较典型。

首先不考虑使用栈，这个题目先应该想到暴力解法。即双重遍历所有的柱子作为边界，然后再找他们之间的最矮柱子，以最矮柱子的高度为矩形的高，边界截取到的宽度为宽，求面积即为可以组成的矩形的最大面积。

Code1

class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < heights.length; i++) {
            for (int j = i; j < heights.length; j++) {
                int minHeight = Integer.MAX_VALUE;
                for (int k = i; k <= j; k++) {
                    minHeight = Math.min(heights[k], minHeight);
                }
                res = Math.max(res, (j - i + 1) * minHeight);
            }
            
        }
        return res;
    }
}

不过这个解答的时间复杂度太高了，会造成TLE问题，通不过。

Algorithm2

暴力解法中，我们对每个区间，找出他们之间最小的高度以及组成的最大矩形，遍历了所有的可能性；这个解法中我们反向去思考，对每个柱子以他为高，找到他能组成的面积最大矩形。

所以以当前柱子为高，他就是那个矩形中最矮的。所以我们找左右边界的话，其实是找左右第一个比他矮的柱子。

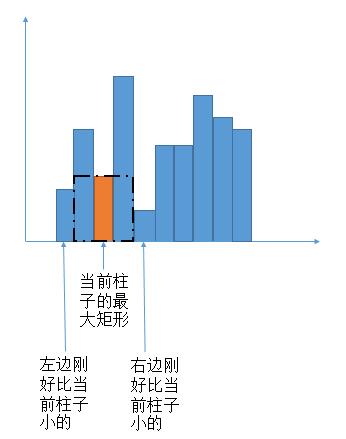
对每个柱子找出这样一组左右边界，最后遍历求最大面积即可。

如何找左右边界，分开来看，看左边（右边同理）：

leftLessMin[0] = -1;//第一个柱子前边没有柱子，所以赋值为 -1，便于计算面积              
for (int i = 1; i < heights.length; i++) {              
    int p = i - 1;
    //p 一直减少，找到第一个比当前高度小的柱子就停止
    while (p >= 0 && height[p] >= height[i]) {
        p--;
    }
    leftLessMin[i] = p;              
}

关键点来了！

这个代码的时间复杂度是$O(n^2)$。但是其实可以优化。

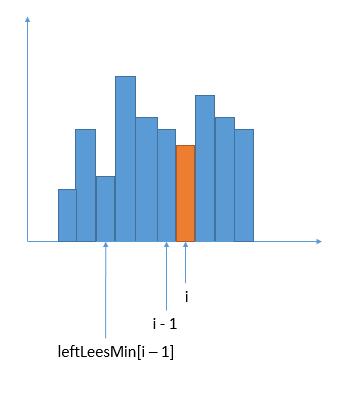
当前柱子i比上一个柱子矮的时候，我们对每个柱子找他的左边界（即那个边界对应位置的柱子是第一个比当前柱子矮的），都是通过index不断减一。但是我们已经找到了上一个前面一个柱子的左边界，我们可以调到上个柱子的左边界对应的柱子高度进行比较。因为从上一个柱子左边界之后的柱子一定比当前柱子高（因为从上一个柱子左边界之后的柱子比上一个柱子要高，上一个柱子比当前柱子高（当前柱子比上一个柱子矮））。

当前柱子i比上一个柱子高的时候，直接就是上一个柱子为左边界。

所以中间那些p--的检查都可以直接跳过。这个也是下个算法中能够使用栈的核心点.

我们之前已经求出了上一个柱子的 leftLessMin[ i - 1]，也就是第一个比上个柱子小的柱子，所以其实我们可以直接跳到 leftLessMin[ i - 1] 比较。因为从 leftLessMin[ i - 1] + 1到 i - 1 的柱子一定是比当前柱子 i 高的，所以可以跳过。

时间也优化到$O(n)$时间。

int[] leftLessMin = new int[heights.length];
leftLessMin[0] = -1;
for (int i = 1; i < heights.length; i++) {
    int l = i - 1;
    //当前柱子更小一些，进行左移
    while (l >= 0 && heights[l] >= heights[i]) { 
        l = leftLessMin[l];
    }
    leftLessMin[i] = l;
}

Code2

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] leftLessMin = new int[heights.length];
        leftLessMin[0] = -1;
        int[] rightLessMin = new int[heights.length];
        rightLessMin[heights.length - 1] = heights.length;
        for (int i = 1; i < heights.length; i++) {
            int left = i - 1;
            while (left >= 0 && heights[left] >= heights[i]) {
                left = leftLessMin[left];
            }
            leftLessMin[i] = left;
        }
        
        for (int i = heights.length - 1; i >= 0; i--) {
            int right = i + 1;
            while (right < heights.length && heights[right] >= heights[i]) {
                right = rightLessMin[right];
            }
            rightLessMin[i] = right;
        }
        
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < heights.length; i++) {
            res = Math.max(res, heights[i] * (rightLessMin[i] - leftLessMin[i] - 1));
        }
        return res;
    }
}

Algorithm3

这个算法其实中心思想和算法2类似，但是使用了栈这个数据结构。

遍历每个柱子，然后分下边几种情况。

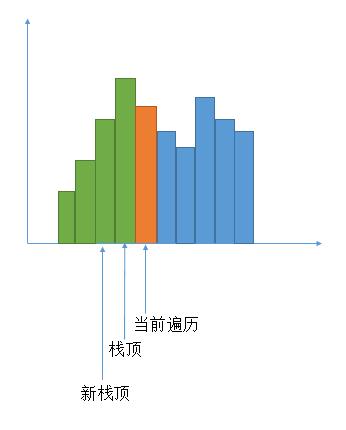
如果当前栈空，或者当前柱子大于栈顶柱子的高度，就将当前柱子的下标入栈
当前柱子的高度小于栈顶柱子的高度。那么就把栈顶柱子出栈，当做当前要求面积的柱子。右边第一个小于当前柱子的下标就是当前在遍历的柱子，左边第一个小于当前柱子的下标就是当前新的栈顶。

遍历完成后，如果栈没有空。就依次出栈，出栈元素当做要求面积的柱子，然后依次计算矩形区域面积。()

Code3

public int largestRectangleArea(int[] heights) {
    int maxArea = 0;
    Stack<Integer> stack = new Stack<>();
    int p = 0;
    while (p < heights.length) {
        //栈空入栈
        if (stack.isEmpty()) {
            stack.push(p);
            p++;
        } else {
            int top = stack.peek();
            //当前高度大于栈顶，入栈
            if (heights[p] >= heights[top]) {
                stack.push(p);
                p++;
            } else {
                //保存栈顶高度
                int height = heights[stack.pop()];
                //左边第一个小于当前柱子的下标
                int leftLessMin = stack.isEmpty() ? -1 : stack.peek();
                //右边第一个小于当前柱子的下标
                int RightLessMin = p;
                //计算面积
                int area = (RightLessMin - leftLessMin - 1) * height;
                maxArea = Math.max(area, maxArea);
            }
        }
    }
    while (!stack.isEmpty()) {
        //保存栈顶高度
        int height = heights[stack.pop()];
        //左边第一个小于当前柱子的下标
        int leftLessMin = stack.isEmpty() ? -1 : stack.peek();
        //右边没有小于当前高度的柱子，所以赋值为数组的长度便于计算
        int RightLessMin = heights.length;
        int area = (RightLessMin - leftLessMin - 1) * height;
        maxArea = Math.max(area, maxArea);
    }
    return maxArea;
}

~~对于栈中剩余元素，因为此时栈中剩下所有的元素是依次增加的，所以后面的元素都是更高的，所以在pop前面越来越小的元素，左边界就是peek，右边界可以一直设为heights数组的长度。~~

其实这个题目还有借助快排思想的做法，但是我更喜欢栈的这个思路，相对我觉得简单点。就不在这写那种解法了。