94. Binary Tree Inorder Traversal

Question

Given the root of a binary tree, return the inorder traversal of its nodes' values.

Algorithm

The recursion is trivial so I implemented only iterative.

So for the in order traversal, we start from a root node and keep push the left to a stack, until there is no left child we then do same thing for the leftmost node in its right child if it has a right child.

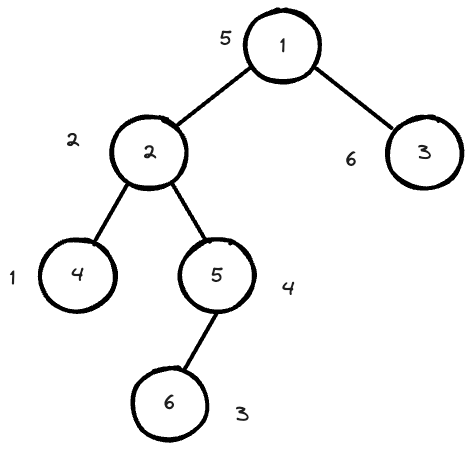
For instance, we start from node1 and push it; then it has left so we keep push the left node2, same as node4,

then node4 has no left so we pop node4 and record it in the result list, and we go to the right of node4 and it has no right;

so we go to another round of pop from the stack; which is node2, then node2 has a right node5 so we push it into the stack and make it as cur, so another round of "find lefts" starts; node5 and node6 are push into stack; now the node6 is on the top of stack;

Pop node6, it has no left and right, thus recorded in the result and the stack keep popping;

Now it's node5, no right, recorded; keep popping, next is node1;

Node1 recorded, it has right, push node3;

Then pop node3, record.

Nothing left in the stack, done;

In the below graph, the number outside the tree is the sequence of the node being popped and calculated.

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if (root == null) return list; 
        Stack<TreeNode> stack = new Stack();
        TreeNode cur = root;
        stack.push(cur);
        while (!stack.isEmpty()) {
            while (cur.left != null) {
                cur = cur.left;
                stack.push(cur);
            }
            TreeNode node = stack.pop();
            list.add(node.val);
            if (node.right != null) {
                stack.push(node.right);
                cur = node.right;
            }
        }
        return list;
    }
}