96. Unique Binary Search Trees

QUESTION

Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.

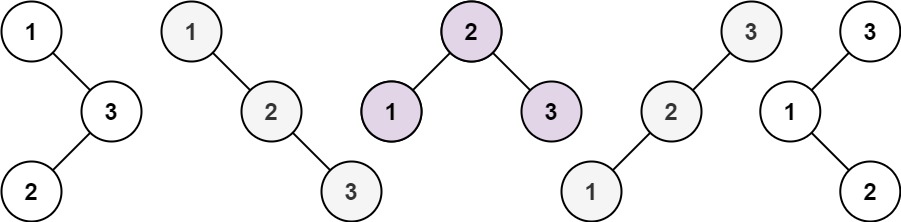
Input: n = 3
Output: 5

ALGRITHOM

By solving this problem recursively we can utilize the code 1's thought, however, it will be a time limit exceeded.

Let's turn our vision to another way.

A key insight here is that you need to realize that the content doesn't matter, the number is what we are utilizing.

We loop each node and regard it as the root, and at that point, the result would be its left unique BST tree count plus its right unique BST count. So we loop all the nodes and add their results together.

The problem can be reduced into problems with smaller sizes, instead of recursively (also repeatedly) solve the subproblems, we can store the solution of subproblems and reuse them later, i.e. the dynamic programming way.

So for DP, the base case is dp[0] = 1, dp[1] = 1; and the status transaction formula is

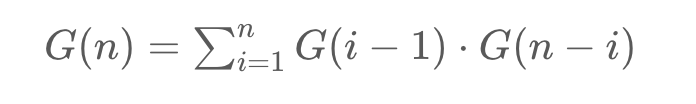
So simply implement the solution.

The problem seems a tree problem but with a dp solution.

The lesson or the key point for the LC question is that you must find the proper way to solve a problem. That's to say, we reading a question, how do you know what approach and data structure and algorithm you will need.

In this question, we firstly use recursion to solve it and find it TEL; in normal pattern we should utilize the memorization and t can be used because the subproblem result is fixed and can be reused.

Then from another perspective, form bottom to top, you may want to use the DP.

The key to this problem is what I said at first, you need to find that the content doesn't matter, the count matters.

Code1(TEL)

class Solution {
    public int numTrees(int n) {
        int res = 0;
        for (int i = 1; i <= n; i++) {
            res += helper(1, i, n);
        }
        return res;
    }
    
    public int helper(int left, int index, int right) {
        if (left == right) return 1;
        int l = 0, r = 0;
        if (left < index) {
            for (int i = left; i < index; i++) {
                l += helper(left, i, index - 1);
            }
        }
        if (index < right) {
           for (int i = index + 1; i <= right; i++) {
                r += helper(index + 1, i, right);
            } 
        }
        return (l == 0 ? 1 : l) * (r == 0 ? 1 : r);
    }
}

CODE2

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}