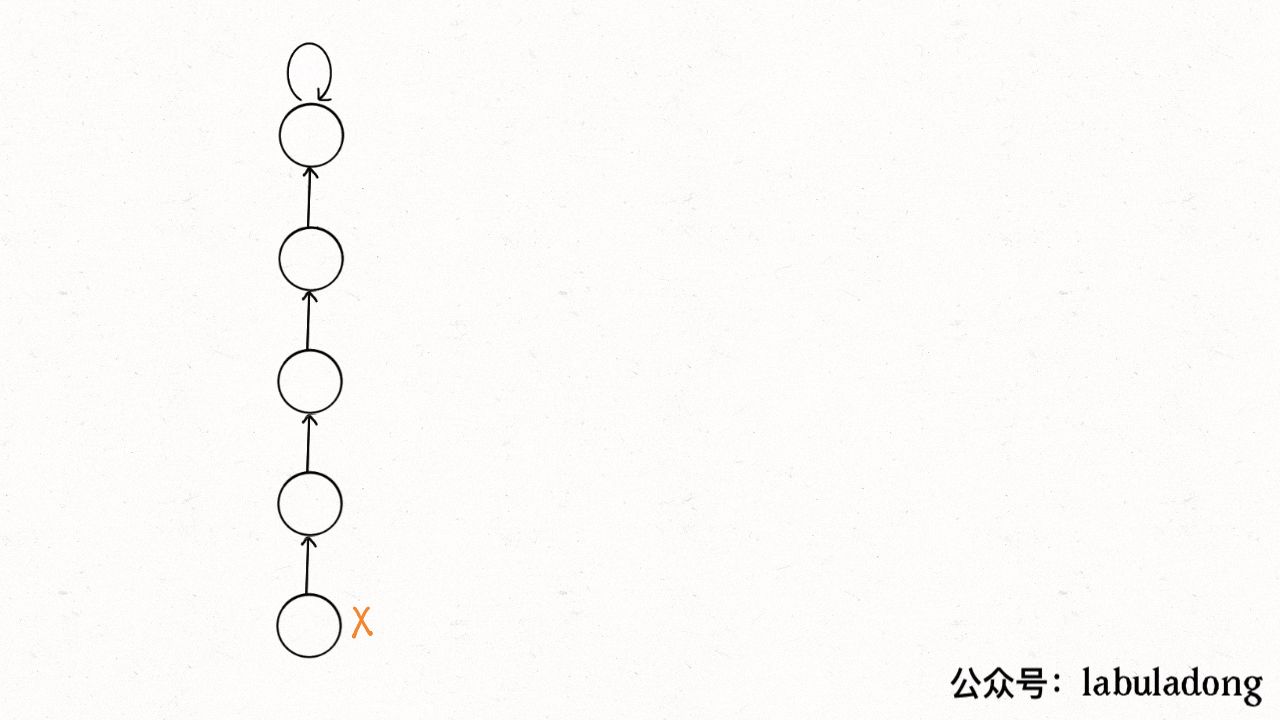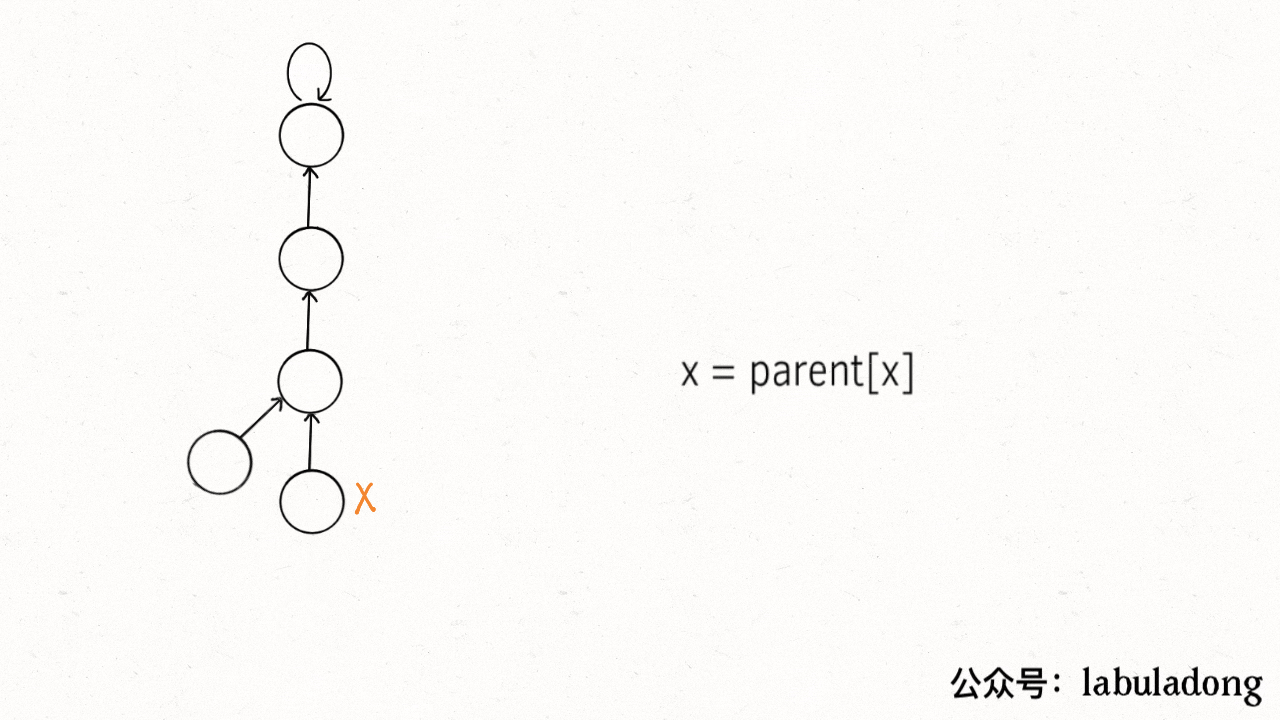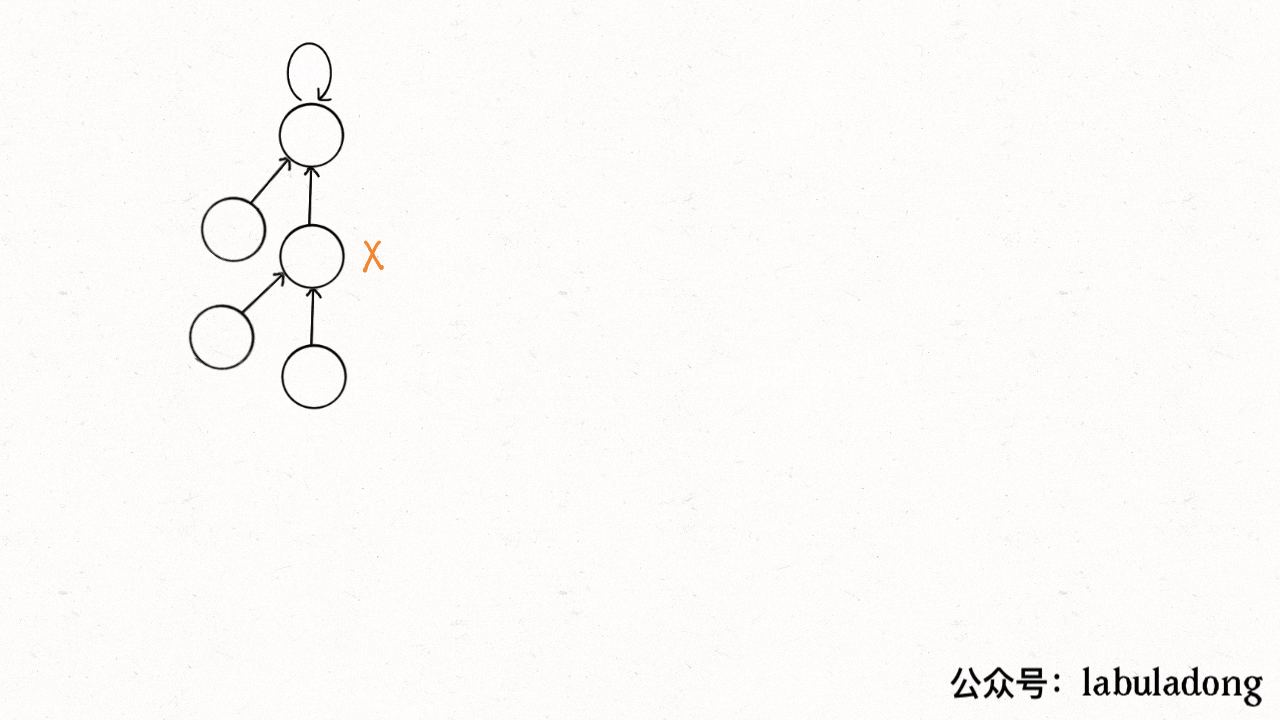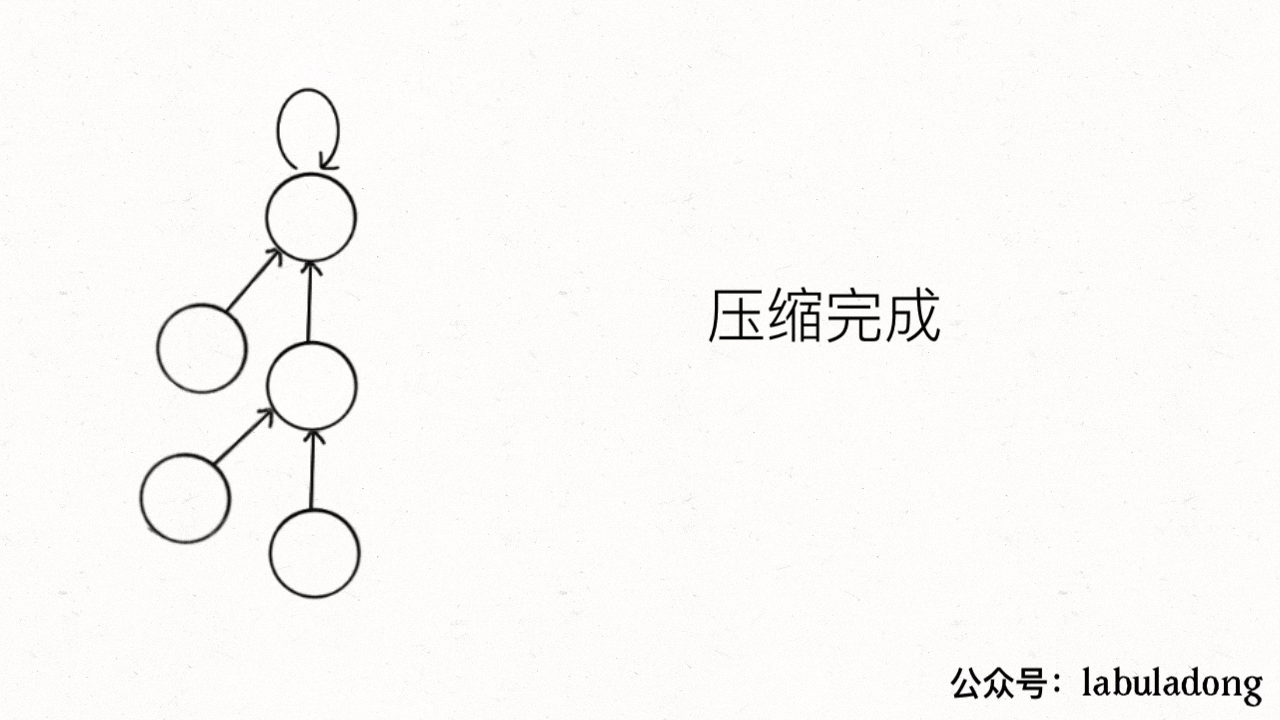Basic
- What is it
A data structure that classify nodes to different sets -> when adding and edge(two vertex) you find they are already in a set, it mean there is a cycle.
Also called disjoint set.
- Why use it
Constant space and time complexity. The key of union find is the efficiency of union() and find()
The precedency of minimum spanning tree.
-
The procedure of build such structure
https://youtu.be/YKE4Vd1ysPI
- At first each node are not connect others
- If two nodes are connected, let one be the parent of the other ;
Implementation
Basic
package Graph.unionfind; public interface IUnionFind { int count(); // how many nodes int union(int x, int y); // merge nodes; int find(int x); // find the corresponded set; boolean connected(int x, int y); // if two nodes connected; }
package Graph.unionfind; public class UnionFindImpl implements IUnionFind{ int count; private int[] id; public UnionFindImpl(int count) { this.count = count; id = new int[count]; for (int i = 0; i < count; i++) { id[i] = i; } } @Override public int count() { return count; } @Override public void union(int x, int y) { int A = find(x); int B = find(y); if (A == B) { return; } for (int i = 0; i < count; i++) { if (id[i] == A) { id[i] = B; } } } @Override public int find(int x) { return id[x]; } @Override public boolean connected(int x, int y) { return find(x) == find(y); } }
Forest Tree representation
Quick Union
Build a tree , connected nodes share same root.
package Graph.unionfind; public class QuickUnion implements IUnionFind{ int count; private int[] parent; public QuickUnion(int count) { this.count = count; parent = new int[count]; for (int i = 0; i < count; i++) { parent[i] = i; } } @Override public int count() { return count; } @Override public void union(int x, int y) { // build a tree int xRoot = find(x); int yRoot = find(y); if (xRoot == yRoot) { return; } parent[xRoot] = yRoot; } @Override public int find(int x) { // find the root; while (x != parent[x]) { x = parent[x]; } return x; } @Override public boolean connected(int x, int y) { return find(x) == find(y); } }
Balance Optimization
Sometimes, the tree may not balance very well and the traverse time become worst O(n) rather than O(logn).
Quick Find Union by Weight
package Graph.unionfind; public class QuickFindUnionByWeight implements IUnionFind{ int count; private int[] parent; private int[] size; public QuickFindUnionByWeight(int count) { this.count = count; parent = new int[count]; for (int i = 0; i < count; i++) { parent[i] = i; size[i] = 1; } } @Override public int count() { return count; } @Override public void union(int x, int y) { // light weight merge to heavy ones; int xRoot = find(x); int yRoot = find(y); if (size[xRoot] > size[yRoot]) { parent[yRoot] = xRoot; size[xRoot] += size[yRoot]; } else { parent[xRoot] = yRoot; size[yRoot] += size[xRoot]; } } @Override public int find(int x) { while (x != parent[x]) { x = parent[x]; } return x; } @Override public boolean connected(int x, int y) { return find(x) == find(y); } }
Quick Find Union by Rank
package Graph.unionfind; public class QuickFindUnionByRank implements IUnionFind{ int count; private int[] parent; private int[] rank; public QuickFindUnionByRank(int count) { this.count = count; parent = new int[count]; for (int i = 0; i < count; i++) { parent[i] = i; rank[i] = 1; } } @Override public int count() { return count; } @Override public void union(int x, int y) { // lower rank merge to higher ones; int xRoot = find(x); int yRoot = find(y); if (rank[xRoot] > rank[yRoot]) { parent[yRoot] = xRoot; } else if (rank[xRoot] < rank[yRoot]){ parent[xRoot] = yRoot; } else { parent[xRoot] = yRoot; rank[yRoot]++; } } @Override public int find(int x) { while (x != parent[x]) { x = parent[x]; } return x; } @Override public boolean connected(int x, int y) { return find(x) == find(y); } }
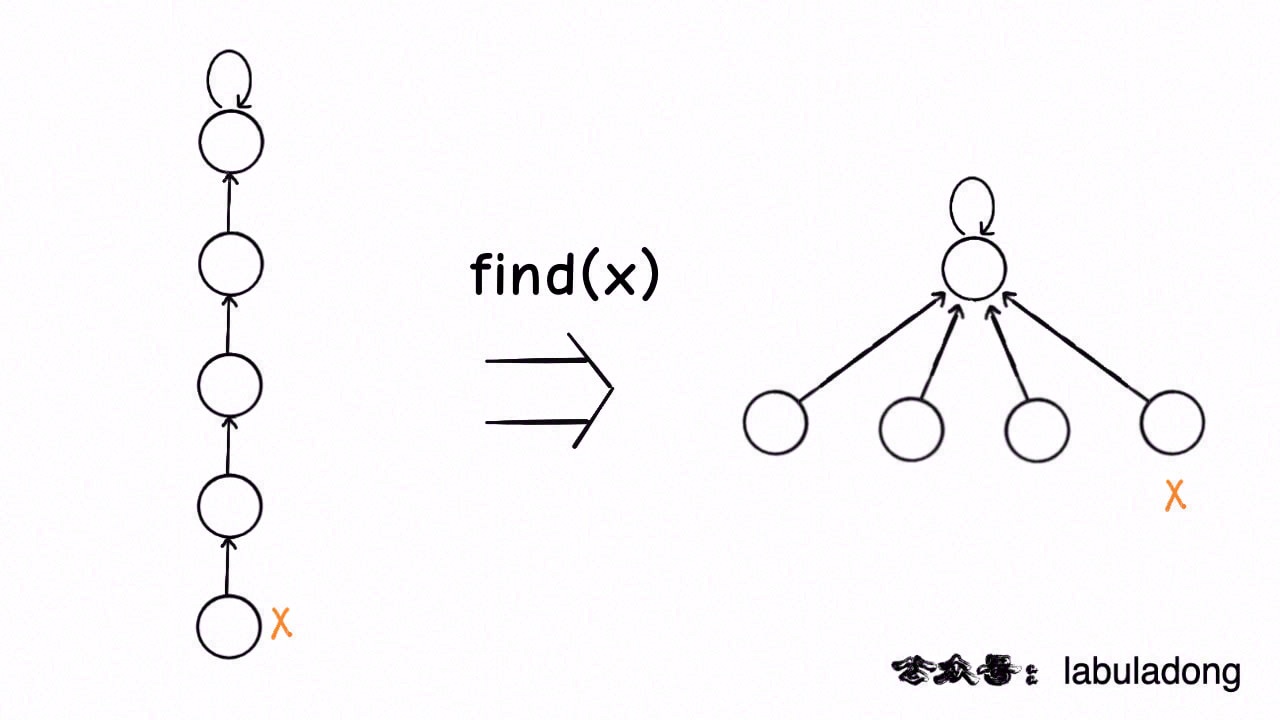
Path Compression
Why we are doing this? Because we actually only care about what the root is each tree. So we are thinking if we could compression the height of the tree and keep it a constant?
Yes we can. There are two ways
package Graph.unionfind; public class QuickFindPathCompression implements IUnionFind{ int count; private int[] parent; public QuickFindPathCompression(int count) { this.count = count; parent = new int[count]; for (int i = 0; i < count; i++) { parent[i] = i; } } @Override public int count() { return count; } @Override public void union(int x, int y) { // quick union, pass } @Override public int find(int x) { // pick one of find or find2 while (x != parent[x]) { parent[x] = parent[parent[x]]; x = parent[x]; } return x; } public int find2(int x) { if (x != parent[x]) { parent[x] = find2(parents[x]); // find the root recursively, more aggressive, make the root as father and all the other nodes, children } return parent[x]; } @Override public boolean connected(int x, int y) { return find(x) == find(y); } }
If you do the second path compression, you may notice balance does not matter anymore so if you use second path compression, you don't need do the balance by size in the union.