-
When solving the leetcode 176 Valid Perfect Square, someone introduced a way to find the root of a high class functions.
-
The main idea is by doing tension again and again, we coud get a solution that is close to the root in a accepatble difference.
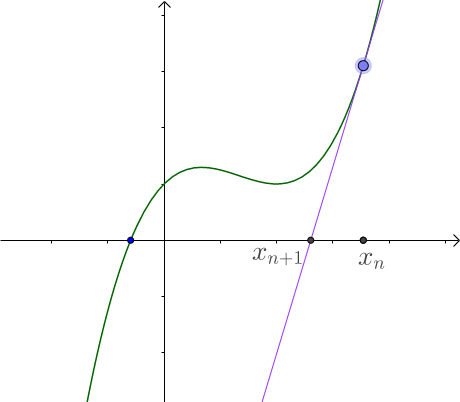
-
So the linear function for the purple line is: $y = f(x_{0}) + f'(x_{0}) * (x - x_{0})$, if we want get the next x(n+1), y = 0.
-
So we could get x by move thing to the other side $x = {x_0 - f'(x_0) \over f'(x_0)}$.
-
In that question(leetcode 367), a square is corresbonded to function like: $f(x) = x^2 - n$, $f'(x) = 2x$.
-
So we get $x_{n+1} = {1 \over 2} * (x_{n} + {n \over x_{n+1}})$.
-
And the solution for this question is we continue looking for a value that just equals to the number(n), if exist return true otherwise return false. The code is like:
public boolean isPerfectSquare(int num) { int x = num; while (x * x > num) { x = 1/2 * (x + num / x); } return x * x == num; }
-
There is another thing I want to explain is why we use num as n. From the graph of a square function like: $f(x) = x^2 - num$, we are trying to find a solution for it,
-
Useful links